在做项目的时候，甲方要求节点之间的连接关系如果不是直接相连，而是通过一系列网络设备如路由器才存在的连接关系。那么把中间这些路由器封装起来用一个云节点表示，在画布上拖动这个云节点到链路上，然后将原本节点之间的链路删除，新建两条链路，分别与该云节点相连，如下图所示。

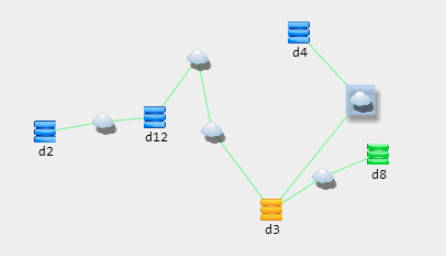
在思考这个问题的时候，云节点拖动的时候判断是否经过某条线路？首先遍历所有的链路，得到链路的两端节点的坐标，分别为(x1,y1)，(x2,y2)。我们把节点的两端看作质点，云节点相当于一个矩形，这时问题就描述成一个数学问题了：如何判断一个矩形跟一条线段有交点？

跟同学交流的时候，她提出一种方案，因为项目需要，这里的矩形基本上是正方形。计算该正方形的外接圆，判断圆心到线段的距离和圆的半径比较。如果大于半径则不相交，如果等于则相切，如果小于则相交。但是如果正方形的边比较大的，还是有一定的误差的。所以就没采用这种方法。

方案二：线段与矩形相交，则线段一定与矩形的两条对角线中的至少一条对角线有交点。那么反推，线段与矩形的对角线有交点可不可以判定，矩形与线段有交点呢？答案是可以的。其实我们可以先这样，将线段假设成直线，计算它的直线方程，为了避免除法，应这样设定：

(y1-y2)x+(x2-x1)y+x1y2-x2y1=0

然后判断对角线是否与该直线相交，将对角线的两个点坐标带入直线方程，乘积<=0则相交。接下来则去除矩形在线段某一侧的情况就ok了，代码如下：

var links = scene.links;for (var i in links)     if (links[i].nodeA && links[i].nodeZ) {    //线段的端点坐标        var x1 = links[i].nodeA.x;    	var y1 = links[i].nodeA.y;    	var x2 = links[i].nodeZ.x;    	var y2 = links[i].nodeZ.y;    	//直线方程设(y1-y2)x+(x2-x1)y+x1y2-x2y1=0    	var a = y1-y2;    	var b = x2-x1;    	var c = x1*y2-x2*y1;	if ((a*target.x+b*target.y+c)*(a*(target.x+target.width)+b*(target.y+target.height)+c)<=0 || 	(a*target.x+b*(target.y+target.height)+c)*(a*(target.x+target.width)+b*target.y+c)<=0) {	if ((x1
    
     
      (target.x+target.width) && x2>(target.x+target.width)) || 	((y1
      
       
        (target.y+target.width)) && (y2>(target.y+target.width)))) {        }	else { //相交	    break;	}    }}
       
      
     
    

其实这个代码有个bug，就是如果这两条链路相交，而云节点拖动到交点处又该如何处理呢？